羅家聰

　　經過疫情大爆、股市大插、經濟大縮，似乎皆黑天鵝。有指美國失業率將見30%，果真如此便是自1890年有紀錄以來所未見;大蕭條時最高還不過是25%。至於股災，四星期內一浪跌近四成的，史上也僅1929和1987年試過;即使2008年也沒這樣急。換言之，這是卅幾至五十幾年才一遇的。至於死過百萬人的瘟疫，對上幾次為1889、1918、1957和1968年，也大約是卅幾至五十幾年一遇。應怎樣理解這些偶發事件?

　　對於事件發生的概率，若一無所知性質不確定的(uncertain)，無法作任何計算，即有估無計。若概率性質可知，則可計算風險(risk)，背後的統計分布通常未必知道，但只要樣本夠大，按中央極限定理都可假設為正態分布。一個統計分布需要兩個描述：集中趨勢和分散度;前者多數用平均或中位值，後者則用標準差。均值很多人都識計，但對於幾多個標準差則未必掌握。聽過6-sigma嗎？就是這個，很關鍵的。是怎樣?　　

　　中學有教，均值(μ)正負1個標準差(σ)已覆蓋68%可能性(對稱每邊34%)，正負2個標準差已涵蓋95%，3個則99%。故一般統計測試也以95%或99%為可信區，實是正負2或3個標準差。譬如將股市畫對數通道取正負兩個標準差，便覆蓋了95%日子，當跌出通道外便是100日當中的5日了，其中2.5日是升穿通道，2.5日跌穿。換言之，在一年約250交易日裏跌穿通道的僅6日，照計入市也不會買貴得到哪裏?

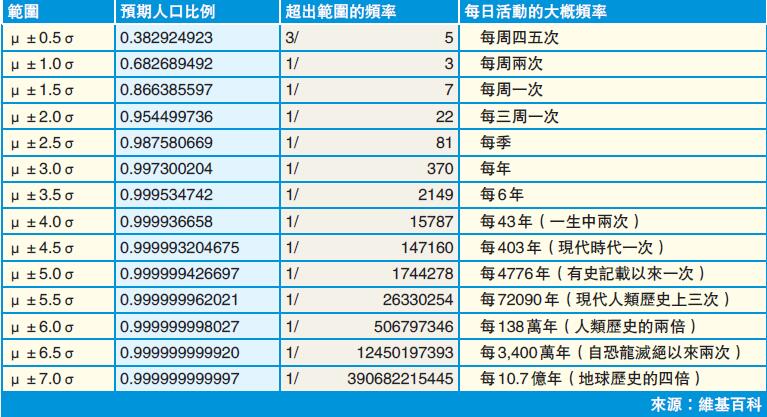
　　未必。以道指由海嘯後牛市起畫對數通道，若一個月前跌穿兩個標準差即25000點便買，結果捱價到18000點，現仍太低水成大閘蟹貨。這關乎跌市背後的風險計算。如文初指，是次瘟疫幾十年一遇，對比附表，這顯然不應以2個標準差即每六周一次計(三周是雙邊，故要除以2)，而應取正負3.5至4個標準差即十幾至幾十年一遇計。結果是，道指跌穿6個標準差才反彈。

　　facebook.com/kachung.law.988

　　lawkachung@gmail.com